DQNなどのDeep Networkを使った強化学習は高い性能を実現するなど成功しているが、人間がタスクを学習するのに比べると多くのデータが必要になるという問題がある。 Pritzel らの提案するNeural Episodic Controlは学習初期におけるデータ不足をDND(Differentiable Neural Dictionary)というKey-Value型の記憶域に蓄積したデータを用いることで改善する。

Pritzelによる解説 が分かりやすかったため、それをベースにまとめる。 本記事の図表はすべてPritzelの記事からそのまま引用しているものである。 論文 arXiv

エピソード記憶の効果 

人間の記憶にはDeclarative memory(明示的な記憶)とprocedural memory(非明示的な記憶)がある (例えば、前者はロンドンがUKの首都であるという知識、後者は自転車の乗り方)。 さらに、Declarative memoryには episodic memory(エピソード記憶)とsemantic memory(意味的記憶)がある (前者は過去にあったことの記憶、後者は単語の意味を知っているとか、一般的な知識)。 なぜこのように人間は一般化された知識だけでなく、エピソードを記憶しているのだろうか？

LengyelとDayanは、長期的な報酬を最大化するためには、シーケンシャルな意思決定が必要になるが、そこに以下のトレードオフが存在するという仮設を立てた。

  • Semantic memory は経験をうまく活かす(より効率的にする)
  • Episodic memory は経験数が少ないほうがいい(それぞれの経験をより詳細に覚えていたい)

これは2つのDeclarative memoryが補い合っている関係にあることを示唆している。

検証のため、tree-structured Markov Decision Process (tMDPs) という、 MDPをツリー状に展開した問題において以下の3種類のエージェントの性能が比較された。

  • 計算にノイズが含まれないモデルベースのエージェント(パフォーマンスの上限を見るため)
  • ノイズが含まれるモデルベースのエージェント
  • モデルフリーのエピソードを利用するエージェント

比較により、2つのことが明らかになった。

  • 報酬の分散を大きくするとあるパフォーマンスを実現するまでの試行数が増加した。
    • => 環境が複雑になると、モデルベースの方法ではより多くの学習データが必要になる。
  • エピソード型のエージェントは少ない試行数のうちはモデルベース型のエージェントより良い性能を示した。この傾向は報酬の分散が大きくなるにつれて顕著になった。

Model-Free Episodic Control 

Lengyel、Dayanの結果には人間がいかに少ない試行で学習を進めるかの示唆があった。 Model-Free Episodic Control では、エピソード記憶を表現するために、(state, action)の組み合わせに対して、Q値を記録するテーブル状のメモリが用いられた。

メモリから取得できる値を$Q_{EC}(s,a)$として、状態$s$は距離的に関連があると仮定して状態$s$の隣接点$k$を取得する。 Q値の推定値$\hat{Q_{EC}(s_t, a_t)}$は以下のようにする。

\begin{equation} \hat{Q_{EC}(s_t, a_t)} \leftarrow \left\{ \begin{aligned} \frac{1}{k} \sum_{i=1}^k Q_{EC}(s^{(i)}, a_t) \text{ if } (s,a) \notin Q_{EC}\\
Q_{EC}(s, a) \text{ if } (s,a) \in Q_{EC}\\
\end{aligned} \right. \end{equation}

近隣$k$状態を用いて近似することで、経験したことのない $(s,a)$の組み合わせに対してもエピソードからQ値を推定している。

また、生理的研究によって、海馬は視野からの入力をそのまま処理していないことがわかっていたため、エピソード記憶の前段の部分に、生の観測$o_t$から状態$s_t$へのマッピング$\phi$を介すようにした。 \begin{equation} s_t = \phi (o_t) \end{equation}

著者らは2種類のマッピングを使うようにした。

  • Model-Free Episodic Controller Random Projection (MFEC-RP)
    • $\phi : o \rightarrow Ao$ というようなランダムに次元を投影する変換
  • Model-Free Episodic Controller Variational Autoencoder (MFEC-VAE)
    • Variational Autoencoderを用いた変換

2種類のMFECはAtari-2600ゲームでテストされ、データ数が少ない領域(frame < 20milion)のときに、DQNやA3Cの性能を凌駕した。

MFEC

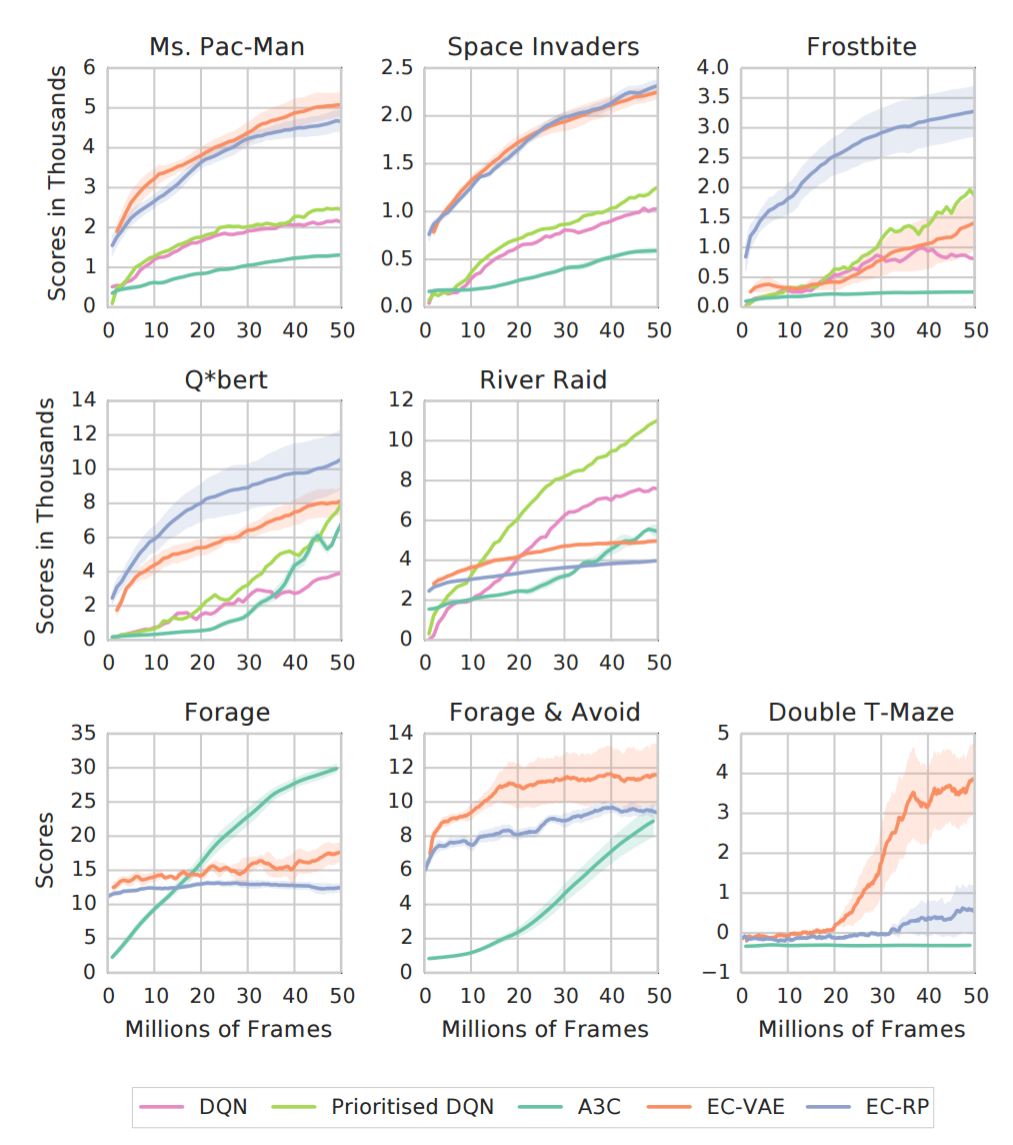
Neural Episodic Control 

Model-Free Episodic Controlの手法をより洗練させたのが、Neural Episodic Control(NEC)である。 NECでは、行動$a$ごとに以下のようなネットワークを割り当てて用いる。

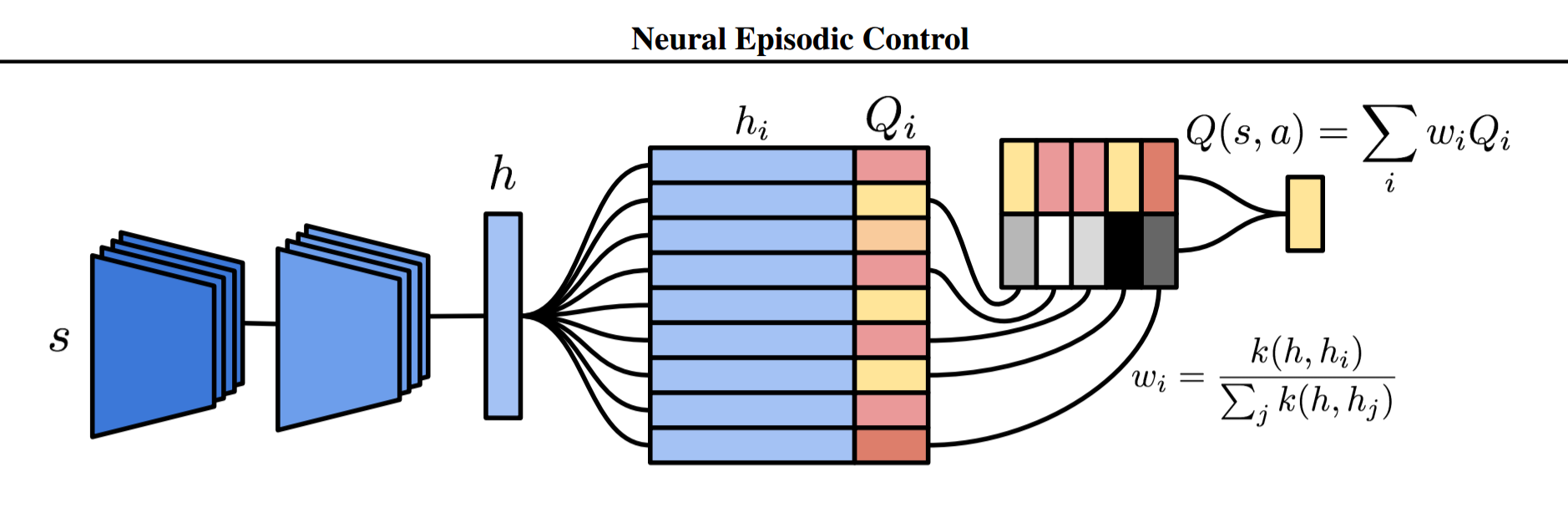
NEC complete

前段は生の画像入力から、状態を簡潔に表現する潜在変数$h$に投影するためのCNNである。 このCNNにはDQNと同じものが用いられている。 その後段でDifferentiable Neural Dictionar(DND)というメモリに入力される。 DNDは以下のKeyとValue型の辞書型メモリである。

\begin{equation} M_a = (K_a, V_a) \end{equation}

$M_a$というように行動$a$のsubscriptが付いているのは、それが行動$a$のためのメモリであることを表している。 $K_a, V_a$は学習に従って大きくなる可変長のベクトルであり、この2つの長さは同じで一対一に対応している。 キーとしては潜在変数$h$を用いており、対応するQ値を保持している。

\begin{equation} \begin{aligned} K_a = \{h_0, \dots, h_i, \dots, h_N\}\\
V_a = \{Q_0, \dots, Q_i, \dots, Q_N\} \end{aligned} \end{equation}

DNDからの値の参照 

状態、行動ペア$(s,a)$について、DNDから参照するときは以下の関係に従って値が取り出される。

\begin{equation} \begin{aligned} Q(s, a) = \sum_{i} w_i Q_i \\
w_i = \frac{k(h, h_i)}{\sum_j k(h, h_j)} \\
k(h, h_i) = \frac{1}{\|h - h_i\|^2 + \omega} \\
\end{aligned} \end{equation}

MFECのように未経験の$(s,a)$についても、周辺のエピソードによって重み付けされた値を取り出すことができる。

DNDへの値の追加 

NECではQ値の推定にはNステップの値をを用いている。 \begin{equation} Q^{(N)}(s_t, a) = \sum_{j=0}^{N-1} \gamma^j r_{t+j} + \gamma^N \max_{a’} Q(s_{t+N}, a’) \end{equation}

もし、DNDに$(s, a)$のペアがすでに存在するとき(つまり、キー$h$に対して値$K_a$がある場合)、Q-Learningの要領で、DNDの値を上書きする。

\begin{equation} Q_i \leftarrow Q_i + \alpha (Q^{(N)}(s,a) - Q_i) \end{equation}

$(s,a)$がDNDに存在しない場合は、$Q^{(N)}(s_t,a)$が$V_a$に、$h$が$K_a$に追加される

実験結果 

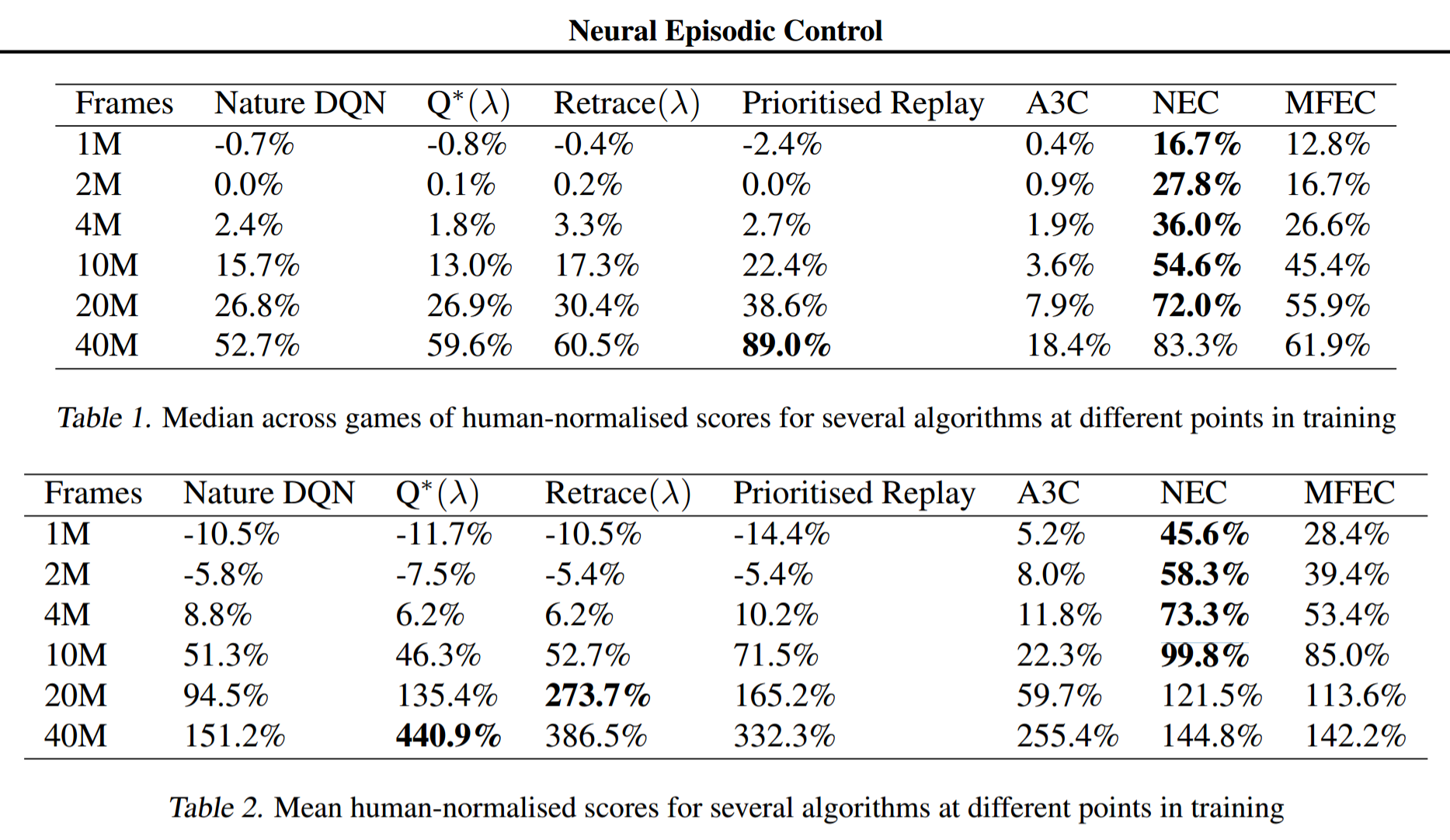
学習フレーム数が少ない段階で、他の手法を凌ぐスコアを達成した。 フレーム数が増えると結果的に抜かされてしまう。 NEC performance table

ただし、MFECとNECには、報酬$r_t$を[0, 1]にクリッピングしなくても学習が安定するという特徴があるため、パックマンでは他手法を凌ぐ高い成果が得られた。 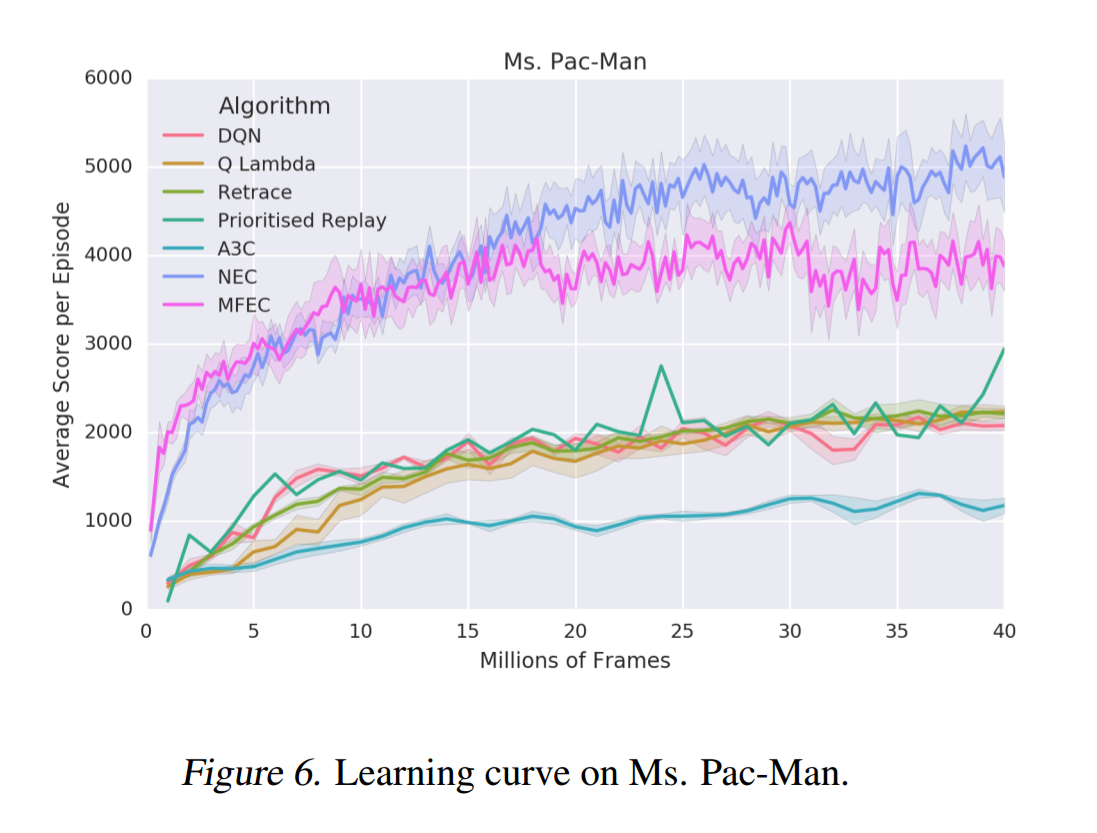NEC pac man パックマンではドットを食べると少し報酬が得られて、ゴーストを食べると大きな報酬が得られるため。

感想 

エピソード記憶を使って学習を早めるのはロボット実機での学習に大いに応用していきたい部分である。 一方で、離散の行動しか扱っていないのが残念だった。 続行動空間への適用はもうひと工夫必要そう。