強化学習について古典的なものからDeepNNを使ったものまでまとめていきたい。

マルコフ決定過程 

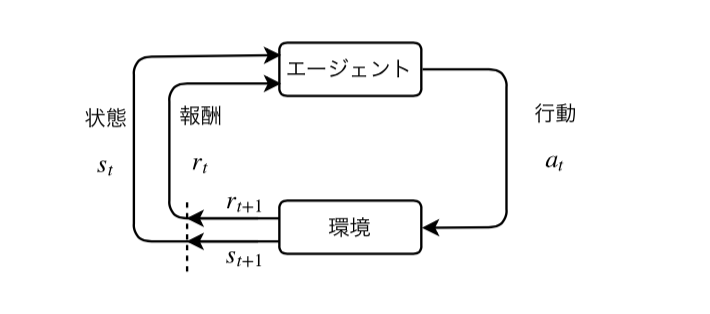
マルコフ決定過程(Markov Decision Process; MDP)は状態の遷移が確率的に起こり、マルコフ過程を満たす過程のことをいう。 MDPは状態$s$、行動$a$、遷移先の状態を$s'$、状態遷移確率$P(s'|s, a)$の組で表現される。 また、状態$s$において行動$a$を選択したとき、即時報酬$r(s, a, s’)$が得られるとする。

とくに時間的な過程の進展を表すため、特に時刻$t$から$t+1$の状態の遷移について

$$ 状態: s_t\\
行動: a_t\\
状態遷移確率: P(s_{t+1}|s_t, a_t)\\
報酬関数: r_t = r(s_t, a_t, s_{t+1}) $$

を考える。

価値関数 

時刻$t$において将来($t \rightarrow \infty $)にわたって得られる報酬について、割引累積報酬$G_t$を定義する。 \begin{equation} G_t = \sum_{k=0}^{\infty} \gamma ^k R_{t+k+1} \end{equation} ここで、$R_{t+1}$は$r(s_t, a_t, s_{t+1})$の値とする。 また、$\gamma$は$0 \le \gamma < 1$の値で、遠い将来に得られるであろう報酬を低く見積もるために使う。

状態$s$において、行動$a$が選択される確率を$\pi = \pi(a | s)$とする。 この$\pi$を方策と呼ぶ。 ロボットで言うと次の状態をどう選ぶかの判断を行う部分である。

さて、ある方策$\pi$を採用したときの報酬がどの程度のものか見積もりたい。 方策$\pi$のもとで、以下のように関数$V^{\pi}$を定義する。 \begin{equation} V^{\pi}(s) = \mathbb{E}[G_t|s_t=s] = \mathbb{E}[R_{t+1}\ + \gamma R_{t+2} + \dots | s_t = s] \label{eq:v_func} \end{equation} これを状態価値関数(あるいは単に価値関数)と呼ぶ。 期待値を取っているのは、方策$\pi$は確率的であるから、$s_t=s$となるのも確率的であるため、$s_t$について周辺化して評価したいためである。

同様に、状態だけでなく、行動についても条件として \begin{equation} Q^{\pi}(s,a) = \mathbb{E}[G_t|s_t=s, a_t=a] = \mathbb{E}[R_{t+1}\ + \gamma R_{t+2} + \dots | s_t = s, a_t = a] \label{eq:q_func} \end{equation} も考える。これを、行動価値関数 と呼ぶ。

以上の枠組みにおいて、最も良い方策、最適方策 を$\pi^{*}$とし、 この方策を採用したときの価値関数を最適行動価値関数 \begin{equation} Q^{*}(s,a) = Q^{\pi^{*}}(s,a) = \max_{\pi} Q^{\pi}(s,a) \end{equation} とする。

ベルマン方程式の導出 

\eqref{eq:v_func}式において$\mathbb{E}[*]$は線形の演算のため、

\begin{equation} \begin{aligned} V^{\pi}(s) &= \mathbb{E}[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} | s_t = s]\\
&= \mathbb{E}[R_{t+1}\ | s_t = s] + \mathbb{E}[\sum_{k=1}^{\infty} \gamma^k R_{t+k+1} | s_t = s]\\
&= \mathbb{E}[R_{t+1}\ | s_t = s] + \gamma \mathbb{E}[\sum_{k=1}^{\infty} \gamma^{k-1} R_{t+k+1} | s_t = s] \end{aligned} \label{eq:q_func_trans} \end{equation}

とすることができる。

ここで、\eqref{eq:q_func_trans}式右辺第1項は

\begin{equation} \begin{aligned} \mathbb{E}[R_{t+1}\ | s_t = s] =\sum_{a \in A(s)} \pi(a|s) \sum_{s’ \in S} P(s'|s, a) r(s, a, s’) \end{aligned} \label{eq:q_func_trans_1} \end{equation}

となる。 $s_t=s$において行動$a$を取る確率が$\pi(a,|s)$、状態遷移して$s'$に移動する確率が$P(s'|s,a)$であるから、行動$a$を取って、状態$s'$に遷移する確率は$\pi(a,|s)P(s'|s,a)$である。 その上で、状態$s$において取れる行動の全集合$A(s)$と次に取れる全状態$S$について$r(s,a,s’)$の期待値を取る、というのが上式で行われていることである。

次に、\eqref{eq:q_func_trans}式右辺第2項は \begin{equation} \begin{aligned} \mathbb{E}[\sum_{k=1}^{\infty} \gamma^{k-1} R_{t+k+1} | s_t = s] &= \sum_{a \in A(s)} \pi(a|s) \sum_{s’ \in S} P(s'|s,a) \mathbb{E}[\sum_{k=1}^{\infty} \gamma^{k-1} R_{t+k+1} | s_{t+1} = s’]\\
&= \sum_{a \in A(s)} \pi(a|s) \sum_{s’ \in S} P(s'|s,a) \mathbb{E}[\sum_{k=0}^{\infty} \gamma^k R_{(t+1)+k+1} | s_{t+1} = s’]\\
&= \sum_{a \in A(s)} \pi(a|s) \sum_{s’ \in S} P(s'|s,a) V^{\pi}(s’) \end{aligned} \label{eq:q_func_trans_2} \end{equation}

と変形できる。 以上\eqref{eq:q_func_trans}, \eqref{eq:q_func_trans_1}, \eqref{eq:q_func_trans_2} 式により、

\begin{equation} \begin{aligned} V^{\pi}(s) = \sum_{a \in A(s)} \pi(a|s) \sum_{s’ \in S} P(s'|s, a) \left(r(s, a, s’) + \gamma V^{\pi}(s’) \right) \end{aligned} \label{eq:belman_value_func} \end{equation}

が導出される。これをベルマン方程式と呼ぶ。

また、$Q^{\pi}(s,a)$の定義より \begin{equation} \begin{aligned} V^{\pi}(s) = \sum_{a \in A(s)} \pi(a|s) Q^{\pi}(s,a) \end{aligned} \end{equation}

であるから、 \begin{equation} \begin{aligned} Q^{\pi}(s, a) &= \sum_{s’} P(s'|s, a) \left(r(s, a, s’) + \gamma V^{\pi}(s’) \right)\\
&= \sum_{s’} P(s'|s, a) \left(r(s, a, s’) + \gamma \sum_{a \in A(s’)} \pi(a'|s’) Q^{\pi}(s’,a’) \right) \end{aligned} \end{equation}

と行動価値関数についてのベルマン方程式を導出できる。