前回 は方策勾配法のアルゴリズムについてまとめた。 今回も前回同様、アルゴリズムについてまとめるが、 最適解に収束しない方策勾配を用いる方法において、いかに勾配を改良するかという部分に軸を置く。 方策勾配を用いる方法では、方策の更新方向の決定が非常に重要になる。 悪い方策を採用したことで低い報酬しか取れないようにずれてくると、回復が難しくなってしまうからだ。 方策の勾配の決定をKLダイバージェンスに基いて決定する方法やその近似を用いたについてまとめる。

自然勾配 

方策の確率分布のパラメタ$\theta$のうち、あるパラメタ$\theta_1, \theta_2$の距離を$\|\theta_1 - \theta_2\|^2$とする、ユークリッド距離において定めたのが、以下の方策の更新方向であった。

\begin{equation} \hat{g} = E_{\pi}[\nabla_{\theta} \log \pi_{\theta} (a | s) A^{\pi}(s, a)] \label{eq:policy_gradient} \end{equation}

ここで、確率分布間の疑距離をKLダイバージェンスで定めると、自然勾配という勾配方法が導出される。 自然勾配は、通常の勾配にフィッシャー行列の逆行列を掛けたものになる

\begin{equation} \tilde{\nabla_{\theta}} J (\theta) = F^{-1} (\theta) \nabla_{\theta} J(\theta) \end{equation}

ここで、$F(\theta)$はフィッシャー行列である。 一般的に、勾配法において、自然勾配を用いると良い性能が得られることが知られている。

Natural Actor-Critic 

式\eqref{eq:policy_gradient}のアドバンテージ関数を線形モデル

\begin{equation} A^{\pi}(s, a) = w^{\mathrm{T}} \nabla_{\theta} \log \pi_{\theta} (a | s) \end{equation} で近似することにすると、

\begin{equation} \nabla_{\theta} J (\theta) = E_{\pi}[\nabla_{\theta} \log \pi_{\theta} (a | s) \nabla_{\theta} \log \pi_{\theta} (a | s) ^ {\mathrm{T}} ] w \\
= F(\theta) w \end{equation}

となる。 さらに方策の勾配として、自然勾配を用いると

\begin{equation} \tilde{\nabla_{\theta}} J (\theta) = F^{-1} (\theta) \nabla_{\theta} F(\theta) w \\
= w \end{equation}

となり、方策はアドバンテージ感数のパラメタ$w$のみを用いて更新できる。

TRPO 

最適化計算における更新ステップの計算にKLダイバージェンスによる制約を加えたものがTRPO(Trust Region Policy Optimization)である。 この方法は、をKLダイバージェンスで拘束しているため、近似的には自然勾配法と同様の手法となる。 TRPOは方策勾配法に限らず、モデルなし学習においても利用することができるが、以下では方策勾配法と組み合わせることを前提に述べる。

さて、$\theta$でパラメタライズされた方策$\pi_{\theta}(a|s)$がある場合、方策勾配が \begin{equation} \hat{g} = E_{\pi}[\nabla_{\theta} \log \pi_{\theta} (a | s) A^{\pi}(s, a)] \end{equation} であった。これは、以下の値$L_{\theta}$の微分値である。 \begin{equation} L_{\theta}(\theta) = E_{\pi}[\log {\pi_{\theta}} (a | s) A^{\pi}(s, a)] \end{equation}

このとき、更新のステップを制限するために、以下のようにKLダイバージェンスで制約を課して最大化を行う。 \begin{equation} \begin{aligned} \underset{x}{\text{maximize }} L_{\theta_{old}} (\theta) \\
\text{subject to } D_{KL}^{\text{max}} (\theta_{old}, \theta) \leq \delta \end{aligned} \end{equation} ここで、$\theta_{old}$は$\pi_{\theta}$におけるパラメタ$\theta$の前の値である。 また、$D_{KL}$は確率分布$\pi_{\theta}$と$\pi_{\theta_{old}}$の間のKLダイバージェンスであり、 $D_{KL}^{\text{max}} (\theta_{old}, \theta)$は任意のパラメタの組み合わせに対して、KLダイバージェンスを計算したときの最大値を表す。 実用的には組み合わせが膨大になり、最大値を求めるのは難しいため、制約はヒューリスティックに以下のように平均値で代用する。 \begin{equation} \begin{aligned} \underset{x}{\text{maximize }} L_{\theta_{old}} (\theta) \\
\text{subject to } \bar{D}_{KL} (\theta_{old}, \theta) \leq \delta \end{aligned} \end{equation} ここで、 $ \bar{D}_{KL} (\theta_1, \theta_2) = E_{s \sim \rho} [D_{KL}(\pi_{\theta_1}(\cdot | s), \pi_{\theta_2}(\cdot | s))] $ である。

ただし、制約において問題を解くのは簡単ではないので、以下のようにソフト制約を使う形に書き下す。 \begin{equation} \underset{x}{\text{maximize }} E_{\pi} [ L_{\theta_{old}} (\theta) - \beta \bar{D}_{KL} (\theta_{old}, \theta) ] \end{equation}

以上が、TRPOの概要である。

PPO 

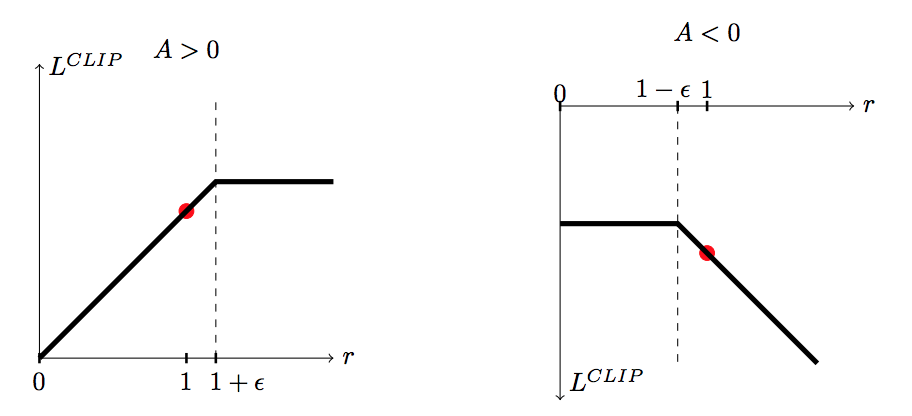
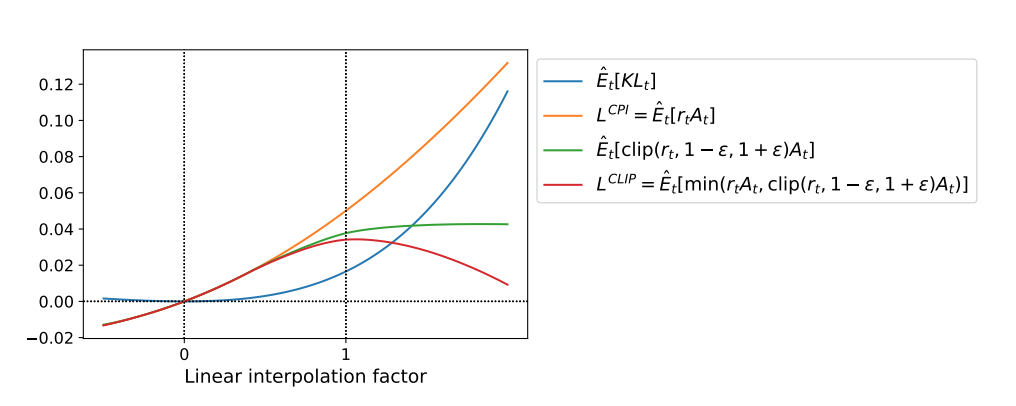
PPO(Proximal Policy Optimization)は方策の目標値をクリッピングすることで、おおまかに方策の更新を制約する方法である。 TRPOではKLダイバージェンスを制約として利用していたが、PPOでは、目的関数を以下の$L^{\text{CLIP}}$として、勾配を求める。

\begin{equation} L^{\text{CLIP}} (\theta) = \hat{E}_t [ \min (r_t(\theta) \hat{A}_t, \text{clip} (r(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t) ] \end{equation}

ここで、$r_t(\theta)$は確率の比率であり、 \begin{equation} r_t(\theta) = \frac {\pi_{\theta}(s_t, a_t)} {\pi_{\theta_{old}}(s_t, a_t)} \end{equation}

である。また、$\text{clip} (r(\theta), 1-\epsilon, 1+\epsilon)$ は、$r(\theta)$が$1-\epsilon$あるいは$1+\epsilon$を超過しないように制限する関数である。 $\text{clip} (r(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t$のグラフと、$L^{\text{CLIP}}$を以下に示す(John Schulmanら¹より引用)。

clip関数	$L^{\text{CLIP}}$

PPOは簡潔なアルゴリズムであるにもかかわらず、高い学習性能を示すことが知られている。