複数の周期的現象が相互作用して同期する現象は実世界のいたるところにみられる。 例えばホタルの発光が同期することはよく知られているし、

バラバラなタイミングで動いていたメトロノームの動きが揃ったり

ロンドンのmillennium bridgeが橋の上で歩いている人々と同期して振動してしまった事件なども同様の現象である。

歩行の周期的運動に着目すると、その生成回路として、CPG(Central Pattern Generator)が知られている。 CPGのモデルを歩行ロボットに組み込む試みも数多くなされている。

本記事ではCPGとその同期について調査し、同期システムを用いた歩行制御についてシミュレーションと実機にて確認した結果について述べる。

背景 

ここでは、まずCPGとニューロンの発火モデル、非線形振動子の同期現象についてまとめる。 また、森本らの振動子の同期現象を2足歩行ロボットの制御に利用した手法について説明する。

CPG 

歩行などのリズミックな運動出力パターンを生成する回路のことをCPGと呼ぶ。 この回路は脊椎動物であれば脊髄に備わっていることが知られている。 大脳との神経的な接続を除去したネコをトレッドミルに乗せ、脊髄部分に電気的刺激を行うと、歩行動作を発現したという、除脳ネコの実験が有名であるが、 この結果より、脳幹部分からの電気的な刺激によって、脊髄部の回路が周期的に活性化し、脚部の筋肉を活性化することで歩行運動が生成されているということを推察することができる。

CPGをモデル化して歩行制御に用いた例としては、多賀¹ による2足歩行運動の生成がある。

ニューロンの発火モデル 

ニューロンは神経系を構成する細胞の一つである。 活動していないときのニューロンの細胞内電位(膜電位)は細胞外に対して低くなっており、逆に活性化すると細胞外に対して高くなる。 この電位差は細胞内外のイオン濃度の差によって生じる。²

HodgkinとHuxleyはヤリイカの巨大軸索の電気的応答を調査することで、そのニューロンの非線形ダイナミクスを記述する微分方程式(Hodgkin-Huxley方程式)を導出した。 詳細は述べないが、4変数でパラメタライズされ微分方程式となっている。³

このHodgkin-Huxley方程式における膜電流(I)として適当な大きさの電流を加えると自励振動が生じる。 宇佐美ら⁴は自励振動に限らず周期的刺激に対するHodgkin-Huxleyのダイナミクスを示している。

Hodgkin-Huxleyより、神経のダイナミクスを更に簡略化したモデルとして、FitzHugh-南雲(FHN)モデルも知られている。

\begin{equation} \begin{aligned} \frac{du}{dt} = u - u^3 -v + I_{ext} \\
\frac{dv}{dt} = u - a - bv \end{aligned} \end{equation}

ここで、$u$がニューロンの膜電位、$v$がニューロン内部の不活性化を表す変数、$a, b$はパラメタである。 このモデルでも同様に周期的振動が生成される。ちなみにパラメタによって興奮性、振動性を示すことが知られている。 フィッツヒュー・南雲 (FitzHugh-Nagumo) 方程式 にてその動作をシミュレーションできる。

en:Balthasar van der Polが電気回路の振動について記述したファン・デル・ポール振動子は、FHNモデルについてa=0, b=0とした場合として理解できる。

以上述べたことは、何らかの生物のCPGの神経回路について直接解析したものではない。 また、実際のCPGは相互作用する複数のニューロンによって構成されており、ニューロン一つの振る舞いだけで説明できるものではない。 しかし、こうした振る舞いの組み合わせとして、CPGのような機能が実現されていると想像することはできる。

非線形振動子 

これまでにニューロンのモデルで示したような周期振動する非線形システムは非線形振動子と捉えることができる。 非線形振動子の特徴としては、その振動がリミットサイクルとして発現することにある。 リミットサイクルとは、相図において特定の軌跡を描く動的安定状態である。 サイクルから外れるような外乱が加わっても元の軌跡に復帰することで安定状態が保たれている。

非線形振動子の同期現象 

復数の非線形振動子に相互作用を行わせると、条件によって同相、逆相で同期することが知られている。 ファン・デル・ポール振動子に対して相互作用の項を加えて振動させると、同期現象を観察できる。

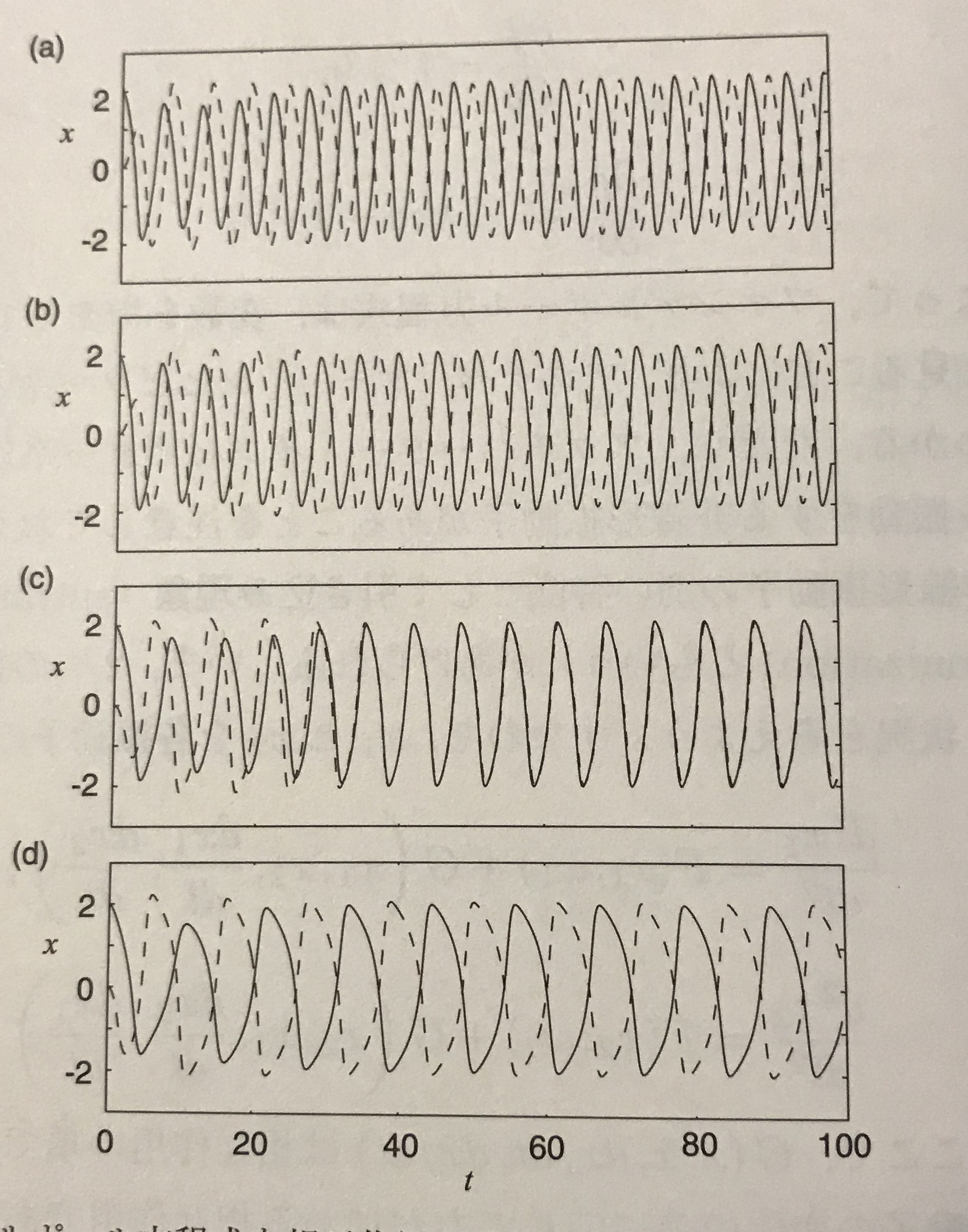画像は蔵本の書籍⁵より引用

周波数は元のどちらのものとも異なるものになる。 このように同期していく振る舞いを引き込み効果と呼ぶ。

蔵本モデル 

同期する非線形振動子のモデルとして蔵本らのモデルが知られている。 以下のサイトで同期現象を視覚的に確認することができる。

Kuramoto-Model Simulator

同期システムを用いた歩行制御 

森本らは、歩行の物理的周期運動と歩行パターンを蔵本モデルで記述し、その相互作用によって外乱に対してアダプティブな歩容が生成されることを示した。^{6 7 8}

ロボットの物理的特性から発現する振動の位相を$\phi_r$、歩行を制御する振動子の位相を$\phi_c$としたとき、以下の結合振動子系を導入する。 ここで、$\omega_r, \omega_c$は固有角振動数、$K_c, K_r$は結合強度である。 物理特性が持つ振動子と、制御器の振動子を同期させるようにしている。

\begin{equation} \begin{aligned} \dot{\phi_r} = \omega_r + K_c \sin(\phi_c - \phi_r) \\
\dot{\phi_c} = \omega_c + K_c \sin(\phi_r - \phi_c) \end{aligned} \end{equation}

ロボットの位相はロボットの足裏のセンサで検出する。 位相の計算には、以下の式が用いられた。

\begin{equation} \phi_{r}(x) = -\arctan \left( \frac{\dot{y}}{y} \right) \end{equation}

ここで、$y$は左右方向の床反力中心位置である。 $y$は両足裏に配置されたセンサによって床反力が左右それぞれ$F^l_z, F^r_z$と検出できるとしたとき、次のように求める。

\begin{equation} y = \frac {y^l_{foot}F^l_z + y^r_{foot}F^r_z} {F^l_z + F^r_z} \end{equation}

ただし、位相検出のためにはスケールは重要でないため、$y^l_{foot} = -y^r_{foot} = 1.0 [m]$としている。

コントローラーの位相のダイナミクスには、次の位相振動子モデルに基づいたものを用いる。 \begin{equation} \dot{\phi_{c_i}} = \omega_c + K_c \sin((\phi_r(x) - \alpha_i) - \phi_{c_i}) \end{equation}

$i={1, \dots ,N}$であり、$N$は関節数を表す。 また、$\alpha_i$は目標位相差である。

ロボットの関節角度は位相$\phi_c$を使って、以下のように決定する。 \begin{equation} \theta^d_i = A_i \sin(\phi_i) + \bar{\theta_i} \end{equation}

$A_i$は各関節の振幅を表すパラメタ、$\bar{\theta_i}$は基準姿勢のためのオフセットを表すパラメタである。

実験 

森本らの手法を参考にして、物理シミュレーション上と実機で実験を行った。

シミュレーション 

物理シミュレーション環境V-REP上で、ヒューマノイドロボットNAOのモデルを歩行させた。 足裏には6次元力覚センサを配置し、$z$方向のみの値を使って、位相を検出した。 パラメタの詳細は、森本らの論文を参照して決定した。

停止状態から足踏みを開始し、歩行を継続できることを確認した。

実機への適用 

足裏センサを用意することができなかったため、加速度センサを使って以下のようにロボットの位相を計測した。

\begin{equation} \phi_{r}(x) = -\arctan \left( \frac{a}{v} \right) \end{equation}

ここで、$a$は加速度センサの値である。 $v$は加速度を積分して求めた。

\begin{equation} v = \int_0^T a dt \end{equation}

ただし、$v$にはドリフトが発生するため、周期的な値であることを利用して、$T$を歩行周期程度に設定した。

停止状態からの足踏みが安定化することを確認した。

一方で、足の踏み出しを行うと、著しく不安定になるため、歩行は実現できなかった。

今後の課題 

実機にて歩行できなかったのは、位相の計測方法に問題があったと思われる。 加速度センサから積分した値を用いるため、位相に時間遅れが発生しているという問題がある。 今後は原論文と同じように足裏にセンサを設置して位相を計測したい。

上体が大きく揺れるような歩容になる結果になったのも、少し不自然であった。 原論文では上体を水平に保つように最適レギュレーターを用いた制御が組み合わされていた。 上体の制御は今後の課題である。

振動子の位相から関節角度に変換する時の振幅やオフセットの調整は難しく、別の対処が必要であると思われる。 強化学習を用いるなどして振幅を学習できないか取り組みたい。